Se realizó el ejercicio 8 de la práctica en grupos y se paso a explicar nuevos circuitos, que fueron

MULTIPLEXOR SIMPLE:

• Proyecta una de las entradas en la salida, a partir la configuración del control.
• Se necesita construir un circuito que permita seleccionar una de sus dos entradas para proyectarla en la salida, en función de una línea de control. Este tipo de operaciones se denomina multiplexación
• Si el control vale 1, se proyecta la entrada e1, y en caso contrario se proyecta e0. Es decir:
  si c=0 entonces s=e0, si c=1 entonces s=e1
• IMPORTANTE: La línea de control es otra entrada mas! Pero lo interesante es que es otro dispositivo el que la setea/configura.

Tabla de verdad:
c | e0 | e1 || s
==================
0 | 0 | 0 || 0
0 | 0 | 1 || 0
0 | 1 | 0 || 1
0 | 1 | 1 || 1
1 | 0 | 0 || 0
1 | 0 | 1 || 1
1 | 1 | 0 || 0
1 | 1 | 1 || 1

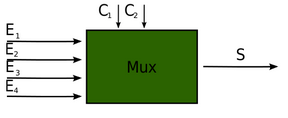
MULTIPLEXOR COMPLEJO:

• Proyecta una de las entradas en la salida, a partir la configuración del control.
• Se necesitan cuatro entradas y dos lineas de control que van a determinar que se proyecta en la salida.
• Si el c0=0 y c1=0 entonces s=e0, si c0=0 y c1=1 entonces s=e1, si c0=1 y c1=0 entonces s=e2, si c0=c1=1 entonces s=e3

DECODIFICADOR:

• Traduce un código de 2 bits de entradas en uno de 4 valores.
• Se necesita un circuito que permita seleccionar un elemento a partir de la cadena binaria que lo identifica, y cada uno de esos elementos está conectado a una de las salidas del circuito. Por ejemplo, si la línea de entrada tiene el valor 0, implica la elección del elemento conectado a la salida s0. En el otro caso, si la línea de entrada tiene el valor 1, implica la elección del elemento conectado a la salida s1.

Tabla de verdad:

e1 | e2 || s0 | s1 | s2 | s3
===|====||====|====|====|=====
0 | 0 || 1 | 0 | 0 | 0
0 | 1 || 0 | 1 | 0 | 0
1 | 0 || 0 | 0 | 1 | 0
1 | 1 || 0 | 0 | 0 | 1

DEMULTIPLEXOR (DEMUX):

• Es el complemento del multiplexor. Permite configurar por que salida se proyecta la entrada.
• Se necesita un circuito que permita compartir una entrada entre varias salidas, en funcion de lo que se configureen el mecanismo de control (que no es más que otro conjunto de entradas).

Se realizaron los ejercicios 19 y 21 de la práctica y se explicó lo que es el producto de sumas (PoS), que es el complemento de la suma de productos (SoP), que es una manera de obtener la fórmula de una tabla de verdad que consiste en multiplicar los terminos correspondientes a las líneas en las que la salida es 0.

Los circuitos aritméticos son circuitos que resuelven tareas específicas,que se relacionan con las operaciones aritméticas entre números que están representados en forma binaria dentro del sistema de cómputos y por lo tanto los circuitos aritméticos operan sobre dos cadenas binarias.
La ALU se puede implementar mediante circuitos, es decir, cada operación aritmética podría ser un circuito.

Se vieron circuitos aritméticos, que son:

HALF ADDER:

Se necesita un circuito que pueda sumar dos cadenas de un bit (BSS(1)) y que calcule el resultado (en BSS(1)) e indique en otra salida si hubo o no acarreo.

Tabla de verdad

e0 | e1 || Suma | Carry
===|====||======|=======
0 | 0 || 0 | 0
0 | 1 || 1 | 0
1 | 0 || 1 | 0
1 | 1 || 0 | 1

FULL ADDER:

Ahora se deben sumar dos cadenas de dos bits cada una (BSS(2)), y ante la imposibilidad de no poder utilizar un half adder, se genera este circuito que permite sumar el acarreo (carry)

Tabla de verdad:

CAnt | e0 | e1 || R | C
=====|====|====||===|====
0 | 0 | 0 || 0 | 0
0 | 0 | 1 || 1 | 0
0 | 1 | 0 || 1 | 0
0 | 1 | 1 || 0 | 1
1 | 0 | 0 || 1 | 0
1 | 0 | 1 || 0 | 1
1 | 1 | 0 || 0 | 1
1 | 1 | 1 || 1 | 1

Se resolvió entre grupos la realización de un circuito restador para BSS(1) con tres entradas (bits a restar y borrow)

Se comenzó la clase resolviendo consultas de los alumnos sobre la práctica 0, de lo que se pasó a realizar en grupos distintas preguntas sobre lógica, que fueron:

1) ¿Que es una tabla de verdad?
2) ¿Para qué sirve una tabla de verdad?
3) ¿Porque las computadoras “usan” el sistema binario?
4) Se tiene la siguiente afirmación: “hoy hace frío, y está nublado o llueve”. Escribir la expresión proposicional usando los conectores lógicos y luego la tabla de verdad

Luego se rotaron las respuestas entre los grupos para hacer devoluciones.

Relacionando con la evolución de la computación (clase 1) en 1938, un tal Shannon del MIT, sugirió utilizar el álgebra de Boole (relacionada con la lógica propocisional) para diseñar circuitos de conmutación y esta idea fue empleada posteriormente en el diseño de circuitos electrónicos (compuertas, que son dispositivos
que implementan (realizan, ejecutan, computan) una función de verdad donde para un conjunto de entradas
se computa (obtiene) una señal de salida).

Las funciones de verdad son un conjunto de proposiciones que indican el valor de verdad de una frase determinada (el mismo puede ser verdadero o falso).

Hay dos tipos de proposiciones, que pueden ser:

• Proposición simple : «Hoy hace frío» (Una proposición con un valor de verdad)
• Proposición compuesta : «Hoy hace frío y esta nublado o llueve», que esta compuesta de expresiones simples unidas por conectores lógicos.

En el caso de las proposiciones compuestas, al tener varias proposiciones se le asigna una letra a cada una y se las une mediante conectores lógicos.

Los conectores lógicos son:

• Conector y: se puede representar con  AND, ^ o  .; es la conjuncion de dos proposiciones.
• Conector o: se puede representar con  OR, ˅, +; es la disyunción de dos proposiciones.
• Conector not: se puede representar con NOT, ¬, es la negación de una proposición.

Ejemplo de proposición y su tabla de verdad:

a = «Hoy hace frio»
b = «Hoy esta nublado»
c = «Hoy llueve»

Proposición compuesta:

a AND (b OR c)

Sin paréntesis se resolvería primero el and [ (a AND b) or C]

Tabla de verdad para esta proposicion: una columna para cada proposicion, lo que daría 2³=8 columnas.

a | b | c || b OR c || r (resultado de a AND f)
0 | 0 | 0 || 0      || 0
0 | 0 | 1 || 1      || 0
0 | 1 | 0 || 1      || 0
0 | 1 | 1 || 1      || 0
1 | 0 | 0 || 0      || 0
1 | 0 | 1 || 1      || 1
1 | 1 | 0 || 1      || 1
1 | 1 | 1 || 1      || 1

IMPORTANTE: mas información sobre los conectivos lógicos puede encontrarse en este apunte

Las tablas de verdad son una herramienta formal para analizar las expresiones mediante la enumeración de sus posibles casos, es decir: las diferentes posibilidades en cuanto a la asignación de valores de verdad (verdadero o falso) a las variables.

Se realizó un ejercicio en grupo, que era graficar la tabla de verdad del AND, del OR y del NOT.
Se realizó una supercompuerta (circuito) que resuelva la funcion a AND (b OR c) con entradas a b y c, un circuito or con b y c y un circuito and con a y resultado del or, con la salida del and como slaida de la supercompuerta.

Aclaración sobre las compuertas:

Al dibujar los circuitos lo recomendable es que las entradas sean en la parte de arriba

Se resolvió en grupo:

1. Diseño de circuitos para expresiones:
   1. ¬ (a ^ b)
   2. ¬ (a ˅ b)
   3. (a ^ ¬ b) ˅ (¬a ^ b)
2. Ejercicio 1 de Práctica 1
3. Ejercicio 5 y 6 – inciso A de Práctica 1

Se realizó el siguiente ejercicio en grupos:
Se necesita un circuito que compare dos entradas (que son las variables de verdad) y que indique si ambas son iguales: ambas verdaderas o ambas falsas.

Se introduce SoP (Suma de productos) a partir de una tabla de verdad, que consiste en juntar en una sola proposición unida con AND y OR aquellas salidas que dan lo que se requiere.

Para la conclusión, en grupos se realizó el siguiente ejercicio:
«Un amigo me regaló el siguiente circuito y me dijo que  su función era la de disparar una alarma en una habitación con dos sensores: uno en la única ventana y otro en la única puerta. Si se abre la ventana, la alarma debe sonar de inmediato, pero si se abre la puerta entonces comienza a correr un reloj que activa la entrada R luego de 5 segundos.»

¿Cómo se comprueba que el circuito cumple con su función?

Se comenzó la clase con dudas que hayan tenido los alumnos con respecto a los temas vistos en la clase anterior, luego de esto se les pidió que respondieran las siguientes preguntas en grupo:

• ¿Cómo se interpreta la cadena 1101?
• ¿Cómo se hace para representar el número 9 en binario?
• Supongamos que utilizamos un sistema restringido a 3 bits. ¿ Qué cantidad de cadenas diferentes puede formar?
• ¿ Cual es el valor más chico que puede representar? ¿ Y el más grande?

Luego se explicó lo que es Binario Sin Signo (BSS), que es un sistema de binario sin signo que se encuentra restringido por una cantidad n de bits, el mismo representa los números naturales y el cero.
En los sistemas BSS, hay una cantidad determinada de números que pueden representarse que son las cadenas con todos ceros o todos unos, en el caso de tener un sistema BSS(3) el mínimo sería 000 y el máximo 111, y el  rango de dicho sistema estaría comprendido entre el 0 y el 7. Los rangos se representan con el número mínimo y el máximo separados por una coma entre corchetes.
Si se quisiera representar un número de n – x bits (siendo n y x dos números al azar) en BSS(n) se debería completar la cadena resultante con n-x ceros a la izquierda del primer bit de la cadena.

Luego de esto, se resolvieron los ejercicios 3, 4, 7 y 9 de la práctica 0.

Se realizaron unas preguntas sobre lo que es la suma de números para introducir la suma binaria, que fueron:

• ¿Cómo sumamos a mano?
• ¿Porqué “me llevo uno”?
• ¿Cómo restamos a mano? Escribir un tutorial para resolver la siguiente cuenta 17-9

La suma binaria se utiliza para sumar dos cadenas binarias dadas, de esta manera, la suma de los bits 0 y 0 da 0, la de los bits 0 y 1 da 1 y la de los bits 1 y 1 da 1 y se «lleva» 1 al bit de la izquierda. Un ejemplo de suma:

1011
+ 1011
——-
11111
Luego se introdujo la resta de cadenas binarias, con el ejemplo de restar 17-9. Las consideraciones para la resta son:

• Si se restan 0 y 0 el resultado es 0, al igual que sucede si se restan 1 y 1.
• Si se restan 1 y 0 el resultado es 1.
• Si se restan 0 y 1 el resultado es 1, pero el bit anterior le presta «1» (En realidad le presta dos, y queda la cadena 10, quedando la resta :

10
– 01
—–
01

• Cuando el primer bit en una resta es 0, SIEMPRE se pide un bit prestado a uno imaginario.
• Cuando en la resta hay un carry de bits, el resultado no se puede representar porque el sistema en el que se realizó la resta no lo permite.

Luego se resolvieron por grupos unas sumas y restas en la pizarra.

Se explicó el sistema hexadecimal, cuyos símbolos son los números del 0 al 9 y las letras de la A a la F.
Para interpretar en hexadecimal es como en binario, pero realizando multiplicaciones suscesivas en base 16.
I(12A) = 1 x 16^2 + 2 x 16^1 + A x 16^0 = 256 + 32 + 10 = 298

Y para representar una cadena también es como en binario pero se divide sucesivamente por 16 y luego se agrupan los restos del último al primero.

Se explicó lo que es la agrupación de bits, que es un método para pasar de binario a hexadecimal, que consiste en agrupar bits en conjuntos de a cuatro para interpretarlos y obtener un valor del sistema hexadecimal; este proceso a la inversa (interpretar un carácter en hexa) se utiliza para pasar de hexadecimal a binario.

Se realizaron los ejercicios 5 y 8 de la práctica 0

Cada grupo realizó un mapa conceptual de la clase y con eso concluyó la misma.

Se realizo la presentación de los alumnos brindandole un post it a cada uno para poder reconocer sus nombres y lo mismo se realizó con los profesores y ayudantes.

Se resolvieron unas preguntas sobre el cuento de los panes en ocho grupos armados al azar por los mismos alumnos, luego de realizarse la puesta en común de las respuestas dadas se mostró el video de la evolución de las computadoras, que se encuentra disponible acá

Se realizó una puesta en común de este video realizando una línea de tiempo en el pizarrón para los datos mas importantes.
Se introduce el concepto de la arquitectura de Von Neumann con un gráfico de como esta compuesta.

Luego de tomar un descanso se realizaron preguntas a todos los grupos sobre los sistemas de numeración para realizar una introducción al sistema binario.
Se explicó como interpretar cadenas binarias (compuestas por unos y ceros).
Por ejemplo:

I(011) = 0 x 2^2 + 1 x 2^1 + 1 x 2^0 = 0 + 2 + 1 = 3

Se realizó la explicación de como representar números con el método de las divisiones sucesivas, que consiste en dividir un número hasta que de cero y acumular los restos de esas divisiones, que son los símbolos que forman la cadena.

Para finalizar la clase, cada grupo pasó al pizarrón para resolver interpretaciones y representaciones.