Se comenzó la clase resolviendo consultas de los alumnos sobre la práctica 0, de lo que se pasó a realizar en grupos distintas preguntas sobre lógica, que fueron:

1) ¿Que es una tabla de verdad?
2) ¿Para qué sirve una tabla de verdad?
3) ¿Porque las computadoras “usan” el sistema binario?
4) Se tiene la siguiente afirmación: “hoy hace frío, y está nublado o llueve”. Escribir la expresión proposicional usando los conectores lógicos y luego la tabla de verdad

Luego se rotaron las respuestas entre los grupos para hacer devoluciones.

Relacionando con la evolución de la computación (clase 1) en 1938, un tal Shannon del MIT, sugirió utilizar el álgebra de Boole (relacionada con la lógica propocisional) para diseñar circuitos de conmutación y esta idea fue empleada posteriormente en el diseño de circuitos electrónicos (compuertas, que son dispositivos
que implementan (realizan, ejecutan, computan) una función de verdad donde para un conjunto de entradas
se computa (obtiene) una señal de salida).

Las funciones de verdad son un conjunto de proposiciones que indican el valor de verdad de una frase determinada (el mismo puede ser verdadero o falso).

Hay dos tipos de proposiciones, que pueden ser:

• Proposición simple : «Hoy hace frío» (Una proposición con un valor de verdad)
• Proposición compuesta : «Hoy hace frío y esta nublado o llueve», que esta compuesta de expresiones simples unidas por conectores lógicos.

En el caso de las proposiciones compuestas, al tener varias proposiciones se le asigna una letra a cada una y se las une mediante conectores lógicos.

Los conectores lógicos son:

• Conector y: se puede representar con  AND, ^ o  .; es la conjuncion de dos proposiciones.
• Conector o: se puede representar con  OR, ˅, +; es la disyunción de dos proposiciones.
• Conector not: se puede representar con NOT, ¬, es la negación de una proposición.

Ejemplo de proposición y su tabla de verdad:

a = «Hoy hace frio»
b = «Hoy esta nublado»
c = «Hoy llueve»

Proposición compuesta:

a AND (b OR c)

Sin paréntesis se resolvería primero el and [ (a AND b) or C]

Tabla de verdad para esta proposicion: una columna para cada proposicion, lo que daría 2³=8 columnas.

a | b | c || b OR c || r (resultado de a AND f)
0 | 0 | 0 || 0      || 0
0 | 0 | 1 || 1      || 0
0 | 1 | 0 || 1      || 0
0 | 1 | 1 || 1      || 0
1 | 0 | 0 || 0      || 0
1 | 0 | 1 || 1      || 1
1 | 1 | 0 || 1      || 1
1 | 1 | 1 || 1      || 1

IMPORTANTE: mas información sobre los conectivos lógicos puede encontrarse en este apunte

Las tablas de verdad son una herramienta formal para analizar las expresiones mediante la enumeración de sus posibles casos, es decir: las diferentes posibilidades en cuanto a la asignación de valores de verdad (verdadero o falso) a las variables.

Se realizó un ejercicio en grupo, que era graficar la tabla de verdad del AND, del OR y del NOT.
Se realizó una supercompuerta (circuito) que resuelva la funcion a AND (b OR c) con entradas a b y c, un circuito or con b y c y un circuito and con a y resultado del or, con la salida del and como slaida de la supercompuerta.

Aclaración sobre las compuertas:

Al dibujar los circuitos lo recomendable es que las entradas sean en la parte de arriba

Se resolvió en grupo:

1. Diseño de circuitos para expresiones:
   1. ¬ (a ^ b)
   2. ¬ (a ˅ b)
   3. (a ^ ¬ b) ˅ (¬a ^ b)
2. Ejercicio 1 de Práctica 1
3. Ejercicio 5 y 6 – inciso A de Práctica 1

Se realizó el siguiente ejercicio en grupos:
Se necesita un circuito que compare dos entradas (que son las variables de verdad) y que indique si ambas son iguales: ambas verdaderas o ambas falsas.

Se introduce SoP (Suma de productos) a partir de una tabla de verdad, que consiste en juntar en una sola proposición unida con AND y OR aquellas salidas que dan lo que se requiere.

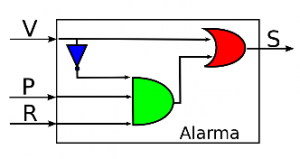
Para la conclusión, en grupos se realizó el siguiente ejercicio:
«Un amigo me regaló el siguiente circuito y me dijo que  su función era la de disparar una alarma en una habitación con dos sensores: uno en la única ventana y otro en la única puerta. Si se abre la ventana, la alarma debe sonar de inmediato, pero si se abre la puerta entonces comienza a correr un reloj que activa la entrada R luego de 5 segundos.»

¿Cómo se comprueba que el circuito cumple con su función?