Archivo por meses: abril 2015

Bitácora-C1-28/04/2015

Posted on por
Comenzamos con un ejercicio individual con entrega. Éste fue tomado de un parcial anterior. Notamos muchos problemas generales a la hora de resolverlo. ¡A practicar y sacarse las dudas!
Luego a la teórica:

SM (Signo magnitud)

  ¿Cómo expresamos un número negativo?
En Q3 un número lo representaremos con una cadena de bits donde el primer bit representará al signo (0 para positivo, 1 para negativo). El resto de la cadena representará la magnitud de la cadena, es decir, el valor del número sin el signo (su valor absoluto).
O sea, la cadena 0011 es el número 3 y 1011 el número –3 ya que lo interpretamos como 1*(-1) + 0*2^2 + 1*2^1 + 1*2^0.
Entonces, ¿cuál es el rango de un SM(3)? El número más grande que podemos expresar es aquel positivo que tenga el mayor absoluto. Como el primer bit es el que usamos para el signo, los otros 2 bits nos quedarán como magnitud. Entonces, la cadena magnitud 11 es la de mayor valor que vamos a poder escribir, lo que nos quedaría junto con el signo en la cadena 011 (o sea, el 3). De esta misma forma, la cadena 111 será la más chica (o sea, el -3).
Las cadenas (con su interpretación) de menor a mayor nos quedarían:
111 (-3)
110 (-2)
101 (-1)
000 (0)
001 (1)
010 (2)
011 (3)
Luego vimos cómo sumar números con signo (tomando en cuenta si ambos operandos tienen o no diferente signo). Recordar: si los operandos tienen el mismo signo podemos sumar normalmente, maneteniendo el signo. Si son de diferente signo podemos hacer la resta entre el número de mayor magnitud y el de menor, así obteniendo el resultado con el signo del primero (de mayor valor absoluto). Al final notamos que ahora cualquier resta en bits la podemos transformar en una suma. O sea, 2 – 3 puede también ser 2 + (-3).
En la segunda parte de la clase estuvimos practicando ejercicios.
A tener en cuenta: Al final de la clase notamos que dejaron sucia el aula, con muchos papeles abandonados. Recuerden que deben dejar limpio el aula! Para la próxima clase los profes estarán atentos a los infractores.

Bitácora-C1-24/04/2015 (Pila y Q3)

Posted on por
Comenzamos la clase con consultas de la practica anterior, y luego se les pidió a los alumnos que en un «post-it» escribieran como creían que funcionaba el CALL y el RET.

Luego se pasó a explicar los siguientes temas:
  • Q3
  • Nueva estructura de datos: Pila
    • La pila esta guardada en una parte especial de la memoria.
    • Nos sirve para apilar y desapilar cosas
    • La operación PUSH nos permite apilar, es decir, agregar un elemento a la pila
    • La operación POP nos permite desapilar, es decir, sacar el ultimo elemento agregado a la pila.
    • El Stack Pointer (SP) nos «dice» cual es el tope de la pila.
  • Implementación del CALL y el RET: El CALL y el RET funcionan utilizando la Pila para guardar la dirección del PC, o bien, para darle una dirección guardada al PC, por lo tanto, en su implementación se usan las operaciones que permiten manejar la Pila
    • El CALL utiliza la operación PUSH, escribiendo un valor en la Pila
    • El RET utiliza la operación POP, leyendo el ultimo valor de la Pila
Para resolver los ejercicios en los que se tiene que realizar un cuadro que muestra como varía el PC, el SP, y la Pila, les recomendamos utilizar la siguiente notación:

Nótese que el PC puede tener dos estados diferentes, uno después de la búsqueda de instrucción y uno después de la ejecución de la instrucción, pero el SP y la Pila no, solo van a cambiar cuando se ejecute la instrucción y solo si la instrucción modifica la Pila, es decir, si la instrucción es CALL o RET.

Este es un ejemplo del cuadro utilizando la notación mencionada anteriormente: main empieza en 1000, rut1 en A0A0, el PC inicial es 1000, la Pila esta vacía.

rut1 : MOV R3, R2
       RET
main: CALL rut1

Para la próxima clase:

¿La arquitectura Q3 permite representar/operar con números negativos?
Si tu respuesta es Si: hacer un programa que inicialice R0 con el valor -1
Si tu respuesta es No: Proponer un mecanismo para extender Q3 y poder hacerlo

Bitácora-C1-21/04/2015 (Rutinas)

Posted on por
Comenzamos con la entrega de parcialitos, repartiéndolos entre los compañeros para que cada uno corrija el de otro.
Resolvimos en grupo ejercicios:
    a) Pensar un programa que calcule: R6 = (95+R1)*18 + R1/(R2+256)
    b) Hacer un programa que calcule n^5 para los números en las celdas A001, A002 y A003 y lo guarde en la misma celda.
Notamos que el primer ejercicio lo podíamos ver como 2 cuentas que se resuelven por separado y luego se suman y el segundo ejercicio como una serie de instrucciones prácticamente idénticas que teníamos que realizar 3 veces (una vez para cada celda).
Entonces, cada una de estas tareas intermedias podemos considerarla una subrutina de nuestro programa.
De esta forma los ejercicios nos quedarían:
    a)
        MOV R3, R1
        ADD R3, 0x005F
        MUL R3, 0x0012
        MOV R4, 0x0100
        ADD R4, R2
        MOV R5, R1
        DIV R5 R4
        MOV R6, R3
        ADD R6, R5
b)
        MOV R1, [0xA001]
        MUL R1, [0xA001]
        MUL R1, [0xA001]
        MUL R1, [0xA001]
        MUL R1, [0xA001]
        MOV R1, [0xA002]
        MUL R1, [0xA002]
        MUL R1, [0xA002]
        MUL R1, [0xA002]
        MUL R1, [0xA002]
        MOV R1, [0xA003]
        MUL R1, [0xA003]
        MUL R1, [0xA003]
        MUL R1, [0xA003]
        MUL R1, [0xA003]
Al separar el programa en partes lo estamos modularizando.
Vemos que el ejercicio b) tiene mucho código repetido (o muy similar). Podemos crear una subrutina más genérica y reusarla para no tener que repetir instrucciones. Para hacerlo, le asignaremos una etiqueta y utilizaremos la noción de parámetros.
Entonces, podemos crear la (sub)rutina:
    elevarA5: MOV R0, R1
                    MUL R0, R1
                    MUL R0, R1
                    MUL R0, R1
                    MUL R0, R1
                    RET
 
Las rutinas etiquetadas deben finalizar con la instrucción RET.
Uso de rutina: Llamamos a una rutina por su etiqueta utilizando la instrucción CALL.
Entonces, el ejercicio b) nos quedaría:
    MOV R1, [0xA001]
    CALL elevarA5
    MOV [0xA001], R0
    MOV R1, [0xA002]
    CALL elevarA5
    MOV [0xA002], R0
    MOV R1, [0xA003]
    CALL elevarA5
    MOV [0xA003], R0
Para utilizar la rituna elevarA5 nos tuvimos que acordar cómo funcionaba o revisar el código para ver qué hacía, qué registros modificaba y dónde devolvía el resultado. De aquí surge la necesidad de documentar nuestro código (o sea, hacer aclaraciones sobre su funcionamiento).
Documentación / Contrato: Toda la información asociada a una rutina la documentamos. La separamos en los siguientes segmentos:
    Requiere: dónde se encuentran los parámetros, cómo y cuáles son       Modifica: Qué variables adicionales modifica
    Retorna: dónde se retorna el resultado
Vimos que también debíamos de especificar cuál es el propósito de nuestra rutina.
Sobre el final de la clase se trabajó con los ejercicios 8,9,11,12,13,14.
Atención con el ejercicio 13: Debemos saber si un número es par. Una forma de conseguir esto es viendo si el resto de la división por 2 es 0. Como no tenemos el operador que nos devuelva el resto, pueden utilizar una supuesta instrucción MOD para ello (que funcionaría como DIV pero devolviendo el resto en vez del cociente).
Luego, pueden crear ustedes mismos la rutina «resto» y cambiar el ejercicio anterior usando la misma.
Entonces, ¿cómo podríamos hacer un programa que calcule el resto? Para pensar. Están advertidos que no será tarea fácil.
Ayuda (Spoilers):
x = (x DIV y) * y + resto (donde DIV es el cociente de la división)
Más ayuda (Spoiler completo):
Si queremos saber el resto de 7 / 3, entonces debemos de calcular el resultado de la división entera de 7 / 3 (que es 2) y multiplicarlo con el divisor (que es 3). Entonces, nos queda 2 * 3 => 6. La diferencia entre este resultado y el dividendo (que es 7) es el resto. O sea, 7 – 6 => 1. Volver a leer la primera ayuda para terminar de entender todo el proceso.

Bitácora-C1-17/04/2015

Posted on por

Se comenzó la clase con unos minutos para consulta de las prácticas

Se pasó a dar los siguientes temas:

  • Cambios en Q
    • Nuevo modo de direccionamiento: «Modo Directo»
  •  Revisión del ciclo de ejecucion de instrucción
    • Decodificación de las instrucciones
      • Registros especiales: Instruction Register (IR) y Program Counter (PC)
    • Busqueda de Operandos
    • Almacenamiento de Operandos
  • Accesos a memoria

Con lo visto en esta clase pueden y deben completar la Guía #3.

Bitácora-C1-14/04/2015

Posted on por
Comenzamos con una etapa de consultas.
Luego comenzamos a ver:
  • Memoria RAM
    • Qué es
    • Cómo funciona relacionada con lo que vimos hasta ahora (Unidad de Control)
    • Celdas de memoria
    • Tamaño de celda
    • Tamaño de memoria
  • Bus del sistema
    • Bus de direcciones
    • Bus de datos
    • Bus de Control
  • Registros
    • Repaso
    • Nuevos (de uso específico, no visibles al programador):
      • MBR (Memory Buffer Register)
      • MAR (Memory Address Register)
  • Q2
    • Se agregan funcionalidades a Q1
    • Nuevo modo de direccionamiento: Directo (la dirección de memoria se especifica entre [ ] en la instrucción)
  • Práctica 3: Ejercicios 2 y 3 entre todos, 4 a 6 en grupos
  • Conclusión: Hicimos un mapa conceptual con los conceptos vistos

Se recordó que debían completar todos los ejercicios de las prácticas anteriores.Para la próxima clase usaremos QSim.

Bitácora-C1-10/04/2015

Posted on por

Se comenzó la clase con consultas de practicas anteriores.
Luego se presentaron los siguientes temas:

Q1

  •  Formato de Instrucciones
    • Códigos de Operación
    • Modos de direccionamiento
    • Partes del formato que por ahora no usamos

Arquitectura de Von Neumann

  • Repaso de la arquitectura: CPU (UC, ALU), Memoria Principal
  • Registros visibles y no visibles al programador (IR- registro de instrucción)
  • Ciclo de Ejecución de instrucciones
    • Búsqueda de instrucción
    • Decodificación de instrucción
    • Ejecución de instrucción
  • Relación con Lógica Digital: MUX8a16, MUX9a16
Al finalizar esto se dejaron ejercicios para resolver en clase (Ejercicios 11, 12, 14, 19, 21 y 23 de la Práctica #2), pero con los conocimientos adquiridos en esta clase se puede resolver toda la  Práctica #2
Se pidió como entrega:
  • Fecha límite: Martes 14/4 a las 8.29
  • Consigna:
    1. Ver video de QSim,
    2. resolver ejercicios 13 y 18 de la práctica 2,
    3. ejecutarlos con el simulador QSim,
    4. hacer capturas de pantalla.
  • Modo de entrega: por mail a mdalponte@unq.edu.ar/flavia.saldana@unq.edu.ar con asunto «(Entrega 3) <Nombre> <Apellido>»

Bitácora-C1-07/04/2015

Posted on por

Logica Digital: Circuitos Aritméticos

En grupos por mesa resolvimos un ejercicio a partir de un enunciado:

Se necesita fabricar el circuito 1de4, que teniendo 4 entradas, su salida valga 1 solo si hay exactamente 1 entrada en 1

  1. Dibujar la “caja negra” del circuito 1de4
  2. Armar la tabla de verdad
  3. Deducir la fórmula de verdad con SOP
  4. graficar las compuertas dentro del circuito

Los circuitos aritméticos son circuitos que resuelven tareas específicas, relacionadas a las operaciones aritméticas entre números. Esos números están representados en forma binaria dentro del sistema de cómputos y por lo tanto los circuitos aritméticos operan sobre dos cadenas binarias. Estos circuitos implementan algunas de las funciones de la ALU (Unidad Aritmetico Logica).

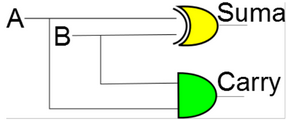
Half Adder: Se necesita un circuito que pueda sumar dos cadenas de un bit (BSS(1)) y que calcule el resultado (en BSS(1)) e indique en otra salida si hubo ó no acarreo.HA

Cuando ejercitamos la suma binaria, distinguimos cuatro casos que nos dan lugar a la siguiente tabla de verdad:

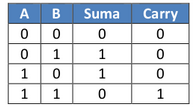tdvHAA cada salida le corresponde una expresión booleana o formula de verdad. Entonces las de este circuito son:

  • s=(a.-b) + (-a.b)
  • c=a.b

De esta manera, se construye el circuito:

HAcmpleto

Full Adder: Supongamos ahora que debemos sumar 2 cadenas de 2 bits cada una (bss(2)). Sería interesante poder usar lo que tenemos en la caja de herramientas: usar dos HA. Sin embargo, el HA no permite arrastrar un acarreo entre las dos columnas. Por ejemplo:01+01 = 10

Pensemos entonces un circuito que sume cadenas en bss(1), pero que también tenga una señal de entrada que indique si hay un acarreo pendiente. La caja negra del circuito es:

FAy la tabla de verdad es como sigue (notar que la primera parte es como el HA, pues este no consideraba acarreo o éste valía 0)

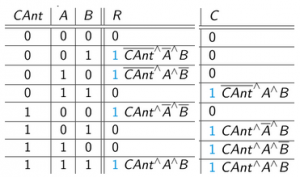
tdvFA

A partir de esto, la expresión SOP de cada salida es:

  • r= noCAnt.(a xor b)+CAnt. no(a xor b)
  • s= noCAnt.a.b+a.CAnt+b.CAnt

 

Sumar múltiples bits: no nos olvidemos que queremos sumar dos cadenas en bss(2). ¿cómo usar el circuito FA que se acaba de definir?

¿En que parte de la computadora se usan estos circuitos? en la ALU. ¿Que/como se alimentan las entradas de la ALU? De eso se encarga la unidad de control.

Ejecucion de programas en la arquitectura Von Neumann

Escribimos una receta en el pizarrón. Vemos que es una secuencia de instrucciones.

El programador es quien escribe la receta según las reglas del manual. ¿eso es todo, el robot (que sigue la arquitectura VN ) de cocina  ya puede cocinar? ¿como? Relacionándolo con temas que vieron en clases anteriores: sabemos que el sistema de cómputos trabaja con circuitos digitales que a su vez se construyen con compuertas binarias, que trasforman entradas digitales.

Surge la necesidad de tener alguna clase de codificación. Proponemos un nuevo manual de cocina ahora si con la codificación.Explicamos que fue necesario traducir cada instrucción.

Si escribimos la receta en código máquina, es una tarea muy engorrosa y propensa a errores con lo cual necesitamos automatizar el proceso. Contamos con un disopsitivo ensamblador cuya tarea es traducir el código fuente a código máquina  y cargarlo en memoria. Las computadoras tienen la capacidad de traducir una cadena binaria en una acción determinada, a través de circuitos digitales!. Eso implica que entre el código fuente y el código máquina hay un ensamblador.

¿y ahora? El usuario pide la ejecución del programa y la cpu ejecuta el mismo con esto tenemos el  ciclo de vida de un programa.

Ahora analicemos en detalle cómo ejecutar una instrucción. Alu es el dispositivo que realiza las operaciones aritmeticas y logicas ¿Hay algún equivalente a la ALU en el juego de la cocina?

Veamos  las siguientes etapas:

  1. La UC (unidad de control) suministra los operandos a la ALU
  2. La UC indica a la ALU la operación a llevar a cabo.
  3. La ALU realiza la operaciónn.
  4. La UC toma el resultado sobre los datos de entrada que se le proveen

Finalmente presentamos un ciclo de ejecución de instrucciones (reducido)

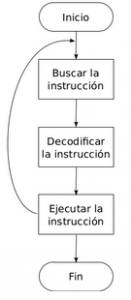cicloreducidoA continuación armamos cajitas con 3 o 4 figuras de huevos dentro, e intentamos volver a preparar una receta pero con las siguientes directivas.

  • Tomar los huevos que hay en la huevera (los que haya ahí)
  • Agregar 1 taza azucar
  • Agregar 1 taza harina
  • Mezclar
  • Hornear medio 10
  1. Ensamblar la receta anterior , deben imaginar un mecanismo para representar la primera instrucción para incorporar al manual.(Ojo que no dejamos ya ocupamos todas las combinaciones con lo cual tienen que imaginar la forma de meter el modo de direccionamiento)

¿Que diferencias hay entre la forma de obtener los ingredientes en la primera instrucción y la segunda? (Vemos que una es variable y otra constante)

Entrega

Construir el circuito restador para BSS(1) (con carry, ejercicio 17):

  1. Dibujar la caja negra del circuito
  2. Construir la tabla (3 entradas)
  3. Construir SOP
  4. Dibujar circuito