Comenzamos la clase con consultas de la práctica 5. A continuación discutimos sobre:

• Rango en Ca2: Calculamos el rango de varios ejemplos de sistemas Complemento a 2.
• La aritmética en Complemento a 2: Comprobamos que al sumar cadenas en Ca2 se debe aplicar el mismo mecanismo aritmético que para cadenas en BSS, y lo comprobamos con los incisos del ejercicio 19, resuelto en el pizarron y corregido por los mismos estudiantes

Sistema Exceso:

1. Dimos una motivación «gráfica» donde las cadenas eran desplazadas sobre la recta de números una cantidad (delta) de lugares. Si delta>0 se desplazan hacia los negativos, y si en cambio delta<0 se desplazan hacia los positivos
2. Vimos a partir de esto como debía ser la interpretación, considerando que es posible utilizar la interpretación en bss:
   Iex(c)=Ibss(c)-delta
3. Dedujimos el mecanismo de representación a partir del mecanismo conocido para la representación en bss. Teniendo en cuenta la dualidad con respecto a la Interpretación, se debe «aplicar» el desplazamiento al número que se quiere representar y luego representar en bss:
   Rex(n)=Rbss(n+delta)
4. Vimos como calcular el rango de un sistema exceso, similarmente a los otros sistemas: interpretando la cadena que representa el mínimo y la que representa el máximo.

Se pide completar la siguiente entrega, con tiempo hasta el lunes 28/9 a las 23.59

El archivo no puede abrirse porque no tienes JavaScript habilitado en tu navegador. Habilítalo y vuelve a cargar el archivo.

Entrega Número 2 - Lógica Digital

*Diseñar un circuito que compare dos cadenas en SM(4) y emita un 1 si son iguales o un 0 en caso contrario.*

Acceder a Google para guardar el progreso. Más información

* Indica que la pregunta es obligatoria

¿Como queda la tabla de verdad del circuito? *

Opcional: Subir la imagen de la formula a un servidor de preferencia y adjuntar el link

Tu respuesta

¿Como queda la fórmula de verdad del circuito? *

Opcional: Subir la imagen de la formula a un servidor de preferencia y adjuntar el link

Tu respuesta

¿Como queda el circuito diseñado? *

Para llenar el campo, subir la imagen a cualquier servidor de preferencia y copiar el link

Tu respuesta

Nombre Y Apellido: *

Tu respuesta

Comisión:

1

2

3

4

Borrar la selección

Dirección de mail: *

Tu respuesta

Enviar

Página 1 de 1

Borrar formulario

Nunca envíes contraseñas a través de Formularios de Google.

Google no creó ni aprobó este contenido. - Condiciones del Servicio - Política de Privacidad

¿El formulario parece sospechoso? Informe

 Formularios

 

 

 

Ayuda y comentarios

•  

   

   
  Ayudar a mejorar Formularios
•  

   

   
  Informe

Hay un nuevo video que explica como instalar QSim en Linux de 64 bits. Pasen y vean!

Entrega (individual):

1. Resolver el ejercicio 20 de la TP3
2. Completar una tabla donde se indique que celdas (o registros) se acceden  en cada etapa del ciclo (BI, BO, AO).

El archivo no puede abrirse porque no tienes JavaScript habilitado en tu navegador. Habilítalo y vuelve a cargar el archivo.

Entrega práctica 3 (accesos en Q2)

Acceder a Google para guardar el progreso. Más información

* Indica que la pregunta es obligatoria

Suponiendo que la celda 0x089A tiene almacenado el costo en pesos de un producto, y la celda 0x089B contiene el porcentaje descuento a aplicar, calcule el valor final de venta a ser almacenado en la celda 0x089C. No puede usar registros para resolverlo. *

Tu respuesta

Completar una tabla donde se indique que celdas (o registros) se acceden  en cada etapa del ciclo (BI, BO, AO). *

Tu respuesta

Nombre y Apellido *

(No usar pseudonimos)

Tu respuesta

Enviar

Borrar formulario

Nunca envíes contraseñas a través de Formularios de Google.

Google no creó ni aprobó este contenido. - Condiciones del Servicio - Política de Privacidad

¿El formulario parece sospechoso? Informe

 Formularios

 

 

 

Ayuda y comentarios

•  

   

   
  Ayudar a mejorar Formularios
•  

   

   
  Informe

Se comenzó la clase con consultas de la primera parte de la práctica de Q1.

Luego, se profundizó sobre lo visto en la clase anterior (Codigo máquina y fuente para las instrucciones).

Proceso de ensamblado:
Para que los programas escritos en Q1 sean ejecutables, deben estar escritos en código máquina, para lo cual se establecen reglas de «traducción» de codigo fuente a codigo máquina para que estas instrucciones sean entendibles por las computadoras.

Esto es conocido como formato de instrucción, que define la organización de los bits dentro de una instrucción. El mismo debe incluir información acerca de las operaciones a resolver y los datos a utilizar (código de la operación y un mecanismo para llegar al/los operando/s).

La estructura para las instrucciones esta compuesta de:
(Operación -4b) (Modo Destino -6b) (Modo Origen -6b) (Destino -16b) (Origen -16b)

Los codigos de las operaciones y modos vistos hasta ahora son:

|——————-|
|Operación | Cod Op |
|==========|========|
| MUL | 0000 |
| MOV | 0001 |
| ADD | 0010 |
| SUB | 0011 |
| DIV | 0111 |
|——————-|
|———————|
| Modo | Cod Op |
|==========|==========|
|Inmediato | 000000 |
|Registro | 100rrr | Donde rrr se corresponde al número del registro a utilizar
|———————|

Según este formato la instrucción ADD R0, 0x0005 se traduce en:
0010 100000 000000 0000000000000101
(CodOp) (modoDest) (modoOr) (Origen)

En este caso, el operando destino no se utiliza porque en Q1 solo puede ser un registro, y esa información siempre se va a encontrar en el modoDest

Para mejorar la legibilidad de las instrucciones, se utilizará una escritura compactada a hexadecimal, de esta manera, la instruccion anterior se escribe 28000005

El proceso inverso (Desensamblado) es el que se realiza en la clase práctica para pasar de una instrucción codificada a una instrucción legible para una persona, el mismo consiste en separar una cadena de bits en codOp, modoDestino, modoOrigen, y operandoOrigen y luego traducirla según la tabla correspondiente.

¿Cómo es la ejecuciòn de programas en esta arquitectura?
1) Al comienzo del ciclo, la UC hace la lectura de instrucción, obteniendo la cadena 28000005
2) La UC decodifica la instrucción, identificando un ADD, que se traduce en una señal a la ALU pidiendo una suma, y una copia de los operandos a las entradas de la ALU. En Q1, el operando destino puede ser uno de los 8 registros (R0 a R7), y el operando origen puede ser además un valor inmediato (que está incluido en la instrucción).
3) La ALU ejecuta la suma y el resultado se dirige a R0.

Luego se proyectó un video de como utilizar QSim (Programa utilizado para simular la ejecución de instrucciones y verificar si un ejercicio esta bien resuelto) y se dedico el tiempo restante de la clase a instalar QSim y terminar la práctica verificando los ejercicios en el simulador.

Se retomó el juego de los panaderos con la salvedad de que las instrucciones ahora poseen códigos, se pide hacer una receta y luego traducirla a los codigos para que un robot inteligente que interpreta las recetas las pueda entender.
Se introducen las nociones de código fuente (comprensible por un humano) y código maquina (que es interpretable por la CPU), los mismos se encuentran relacionados ya que el programador escribe un programa en codigo fuente y que mediante
un interprete se ensambla y pasa a ser código máquina para ser ejecutado en una computadora, en lo que es el ciclo de vida de un programa.

En la arquitectura de VN, la ALU realiza las operaciones aritméticas con operandos suministrados por la UC, la que tambien
le indica a la ALU que operación llevar a cabo, la misma es realizada y la UC toma el resultado sobre los datos de entrada
provistos. Estas son las etapas de ejecución de un programa.

INSERTAR GRAFICO CICLO DE EJECUCION

Luego se agrego una nueva variación a las recetas para ensamblar, que son contar con opciones como:

• Agregar los huevos que hay en la huevera (Los que haya)
• Agregar 3 cucharadas de aceite

De esta manera se introducen los modos de direccionamiento (mecanismo por el cual la UC obtiene el operando requerido), que son:

• Modo inmediato: El valor buscado esta codificado en una constante dentro de la instrucción
• Modo registro: El valor buscado esta en un registro (que es un espacio de almacenamiento interno a la CPU)

Pasa a presentarse Q1, que es una arquitectura «teorica» que se va a utilizar en la materia, la cual cuenta con 8 registros para utilizar, un set de instrucciones que se utilizarán para realizar operaciones entre registros y constantes.
En Q1 se manejan datos de tipo BSS(16).

Los registros a utilizar son el R0, R1, R2, R3, R4, R5, R6 y R7.

Las instrucciones a utilizar son:

Operando | Operación |
=========|======================|
ADD | Suma |
=========|======================|
SUB | Resta |
=========|======================|
MUL | Multiplicación |
=========|======================|
DIV | División Entera |
=========|======================|
MOV | Copia de registros |

Se utilizan de la siguiente manera:

ADD destino, origen = destino <– destino + origen
SUB destino, origen = destino <– destino – origen
MUL destino, origen = (R7, destino) <– destino * origen (Los 16 bits mas significativos en destino, el resto en R7)
DIV destino, origen = destino <– destino % origen
MOV destino, origen = destino <– origen

Los operandos destino u origen pueden ser variables (registros) o constantes (cadenas de 16 bits representadas en hexa con la notacion 0xcadena de bits representada en hexa)

Ejemplos de programas en Q1

ADD R7, 0x0002 ==> Suma el contenido de R7 mas 2
MOV R6, R0 ==> Copia el valor de R0 en R6

Luego se resolvieron los ejercicios del 1 al 19 de la práctica de los cuales los grupos pasaron al pizarrón a resolver los ejercicios 3,4,9,10,14 y 16

Se realizó el ejercicio 8 de la práctica en grupos y se paso a explicar nuevos circuitos, que fueron

MULTIPLEXOR SIMPLE:

• Proyecta una de las entradas en la salida, a partir la configuración del control.
• Se necesita construir un circuito que permita seleccionar una de sus dos entradas para proyectarla en la salida, en función de una línea de control. Este tipo de operaciones se denomina multiplexación
• Si el control vale 1, se proyecta la entrada e1, y en caso contrario se proyecta e0. Es decir:
  si c=0 entonces s=e0, si c=1 entonces s=e1
• IMPORTANTE: La línea de control es otra entrada mas! Pero lo interesante es que es otro dispositivo el que la setea/configura.

Tabla de verdad:
c | e0 | e1 || s
==================
0 | 0 | 0 || 0
0 | 0 | 1 || 0
0 | 1 | 0 || 1
0 | 1 | 1 || 1
1 | 0 | 0 || 0
1 | 0 | 1 || 1
1 | 1 | 0 || 0
1 | 1 | 1 || 1

MULTIPLEXOR COMPLEJO:

• Proyecta una de las entradas en la salida, a partir la configuración del control.
• Se necesitan cuatro entradas y dos lineas de control que van a determinar que se proyecta en la salida.
• Si el c0=0 y c1=0 entonces s=e0, si c0=0 y c1=1 entonces s=e1, si c0=1 y c1=0 entonces s=e2, si c0=c1=1 entonces s=e3

DECODIFICADOR:

• Traduce un código de 2 bits de entradas en uno de 4 valores.
• Se necesita un circuito que permita seleccionar un elemento a partir de la cadena binaria que lo identifica, y cada uno de esos elementos está conectado a una de las salidas del circuito. Por ejemplo, si la línea de entrada tiene el valor 0, implica la elección del elemento conectado a la salida s0. En el otro caso, si la línea de entrada tiene el valor 1, implica la elección del elemento conectado a la salida s1.

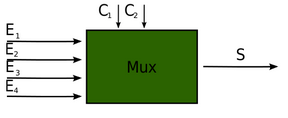
Tabla de verdad:

e1 | e2 || s0 | s1 | s2 | s3
===|====||====|====|====|=====
0 | 0 || 1 | 0 | 0 | 0
0 | 1 || 0 | 1 | 0 | 0
1 | 0 || 0 | 0 | 1 | 0
1 | 1 || 0 | 0 | 0 | 1

DEMULTIPLEXOR (DEMUX):

• Es el complemento del multiplexor. Permite configurar por que salida se proyecta la entrada.
• Se necesita un circuito que permita compartir una entrada entre varias salidas, en funcion de lo que se configureen el mecanismo de control (que no es más que otro conjunto de entradas).

Se realizaron los ejercicios 19 y 21 de la práctica y se explicó lo que es el producto de sumas (PoS), que es el complemento de la suma de productos (SoP), que es una manera de obtener la fórmula de una tabla de verdad que consiste en multiplicar los terminos correspondientes a las líneas en las que la salida es 0.

Los circuitos aritméticos son circuitos que resuelven tareas específicas,que se relacionan con las operaciones aritméticas entre números que están representados en forma binaria dentro del sistema de cómputos y por lo tanto los circuitos aritméticos operan sobre dos cadenas binarias.
La ALU se puede implementar mediante circuitos, es decir, cada operación aritmética podría ser un circuito.

Se vieron circuitos aritméticos, que son:

HALF ADDER:

Se necesita un circuito que pueda sumar dos cadenas de un bit (BSS(1)) y que calcule el resultado (en BSS(1)) e indique en otra salida si hubo o no acarreo.

Tabla de verdad

e0 | e1 || Suma | Carry
===|====||======|=======
0 | 0 || 0 | 0
0 | 1 || 1 | 0
1 | 0 || 1 | 0
1 | 1 || 0 | 1

FULL ADDER:

Ahora se deben sumar dos cadenas de dos bits cada una (BSS(2)), y ante la imposibilidad de no poder utilizar un half adder, se genera este circuito que permite sumar el acarreo (carry)

Tabla de verdad:

CAnt | e0 | e1 || R | C
=====|====|====||===|====
0 | 0 | 0 || 0 | 0
0 | 0 | 1 || 1 | 0
0 | 1 | 0 || 1 | 0
0 | 1 | 1 || 0 | 1
1 | 0 | 0 || 1 | 0
1 | 0 | 1 || 0 | 1
1 | 1 | 0 || 0 | 1
1 | 1 | 1 || 1 | 1

Se resolvió entre grupos la realización de un circuito restador para BSS(1) con tres entradas (bits a restar y borrow)

Se comenzó la clase resolviendo consultas de los alumnos sobre la práctica 0, de lo que se pasó a realizar en grupos distintas preguntas sobre lógica, que fueron:

1) ¿Que es una tabla de verdad?
2) ¿Para qué sirve una tabla de verdad?
3) ¿Porque las computadoras “usan” el sistema binario?
4) Se tiene la siguiente afirmación: “hoy hace frío, y está nublado o llueve”. Escribir la expresión proposicional usando los conectores lógicos y luego la tabla de verdad

Luego se rotaron las respuestas entre los grupos para hacer devoluciones.

Relacionando con la evolución de la computación (clase 1) en 1938, un tal Shannon del MIT, sugirió utilizar el álgebra de Boole (relacionada con la lógica propocisional) para diseñar circuitos de conmutación y esta idea fue empleada posteriormente en el diseño de circuitos electrónicos (compuertas, que son dispositivos
que implementan (realizan, ejecutan, computan) una función de verdad donde para un conjunto de entradas
se computa (obtiene) una señal de salida).

Las funciones de verdad son un conjunto de proposiciones que indican el valor de verdad de una frase determinada (el mismo puede ser verdadero o falso).

Hay dos tipos de proposiciones, que pueden ser:

• Proposición simple : «Hoy hace frío» (Una proposición con un valor de verdad)
• Proposición compuesta : «Hoy hace frío y esta nublado o llueve», que esta compuesta de expresiones simples unidas por conectores lógicos.

En el caso de las proposiciones compuestas, al tener varias proposiciones se le asigna una letra a cada una y se las une mediante conectores lógicos.

Los conectores lógicos son:

• Conector y: se puede representar con  AND, ^ o  .; es la conjuncion de dos proposiciones.
• Conector o: se puede representar con  OR, ˅, +; es la disyunción de dos proposiciones.
• Conector not: se puede representar con NOT, ¬, es la negación de una proposición.

Ejemplo de proposición y su tabla de verdad:

a = «Hoy hace frio»
b = «Hoy esta nublado»
c = «Hoy llueve»

Proposición compuesta:

a AND (b OR c)

Sin paréntesis se resolvería primero el and [ (a AND b) or C]

Tabla de verdad para esta proposicion: una columna para cada proposicion, lo que daría 2³=8 columnas.

a | b | c || b OR c || r (resultado de a AND f)
0 | 0 | 0 || 0      || 0
0 | 0 | 1 || 1      || 0
0 | 1 | 0 || 1      || 0
0 | 1 | 1 || 1      || 0
1 | 0 | 0 || 0      || 0
1 | 0 | 1 || 1      || 1
1 | 1 | 0 || 1      || 1
1 | 1 | 1 || 1      || 1

IMPORTANTE: mas información sobre los conectivos lógicos puede encontrarse en este apunte

Las tablas de verdad son una herramienta formal para analizar las expresiones mediante la enumeración de sus posibles casos, es decir: las diferentes posibilidades en cuanto a la asignación de valores de verdad (verdadero o falso) a las variables.

Se realizó un ejercicio en grupo, que era graficar la tabla de verdad del AND, del OR y del NOT.
Se realizó una supercompuerta (circuito) que resuelva la funcion a AND (b OR c) con entradas a b y c, un circuito or con b y c y un circuito and con a y resultado del or, con la salida del and como slaida de la supercompuerta.

Aclaración sobre las compuertas:

Al dibujar los circuitos lo recomendable es que las entradas sean en la parte de arriba

Se resolvió en grupo:

1. Diseño de circuitos para expresiones:
   1. ¬ (a ^ b)
   2. ¬ (a ˅ b)
   3. (a ^ ¬ b) ˅ (¬a ^ b)
2. Ejercicio 1 de Práctica 1
3. Ejercicio 5 y 6 – inciso A de Práctica 1

Se realizó el siguiente ejercicio en grupos:
Se necesita un circuito que compare dos entradas (que son las variables de verdad) y que indique si ambas son iguales: ambas verdaderas o ambas falsas.

Se introduce SoP (Suma de productos) a partir de una tabla de verdad, que consiste en juntar en una sola proposición unida con AND y OR aquellas salidas que dan lo que se requiere.

Para la conclusión, en grupos se realizó el siguiente ejercicio:
«Un amigo me regaló el siguiente circuito y me dijo que  su función era la de disparar una alarma en una habitación con dos sensores: uno en la única ventana y otro en la única puerta. Si se abre la ventana, la alarma debe sonar de inmediato, pero si se abre la puerta entonces comienza a correr un reloj que activa la entrada R luego de 5 segundos.»

¿Cómo se comprueba que el circuito cumple con su función?

Se comenzó la clase con dudas que hayan tenido los alumnos con respecto a los temas vistos en la clase anterior, luego de esto se les pidió que respondieran las siguientes preguntas en grupo:

• ¿Cómo se interpreta la cadena 1101?
• ¿Cómo se hace para representar el número 9 en binario?
• Supongamos que utilizamos un sistema restringido a 3 bits. ¿ Qué cantidad de cadenas diferentes puede formar?
• ¿ Cual es el valor más chico que puede representar? ¿ Y el más grande?

Luego se explicó lo que es Binario Sin Signo (BSS), que es un sistema de binario sin signo que se encuentra restringido por una cantidad n de bits, el mismo representa los números naturales y el cero.
En los sistemas BSS, hay una cantidad determinada de números que pueden representarse que son las cadenas con todos ceros o todos unos, en el caso de tener un sistema BSS(3) el mínimo sería 000 y el máximo 111, y el  rango de dicho sistema estaría comprendido entre el 0 y el 7. Los rangos se representan con el número mínimo y el máximo separados por una coma entre corchetes.
Si se quisiera representar un número de n – x bits (siendo n y x dos números al azar) en BSS(n) se debería completar la cadena resultante con n-x ceros a la izquierda del primer bit de la cadena.

Luego de esto, se resolvieron los ejercicios 3, 4, 7 y 9 de la práctica 0.

Se realizaron unas preguntas sobre lo que es la suma de números para introducir la suma binaria, que fueron:

• ¿Cómo sumamos a mano?
• ¿Porqué “me llevo uno”?
• ¿Cómo restamos a mano? Escribir un tutorial para resolver la siguiente cuenta 17-9

La suma binaria se utiliza para sumar dos cadenas binarias dadas, de esta manera, la suma de los bits 0 y 0 da 0, la de los bits 0 y 1 da 1 y la de los bits 1 y 1 da 1 y se «lleva» 1 al bit de la izquierda. Un ejemplo de suma:

1011
+ 1011
——-
11111
Luego se introdujo la resta de cadenas binarias, con el ejemplo de restar 17-9. Las consideraciones para la resta son:

• Si se restan 0 y 0 el resultado es 0, al igual que sucede si se restan 1 y 1.
• Si se restan 1 y 0 el resultado es 1.
• Si se restan 0 y 1 el resultado es 1, pero el bit anterior le presta «1» (En realidad le presta dos, y queda la cadena 10, quedando la resta :

10
– 01
—–
01

• Cuando el primer bit en una resta es 0, SIEMPRE se pide un bit prestado a uno imaginario.
• Cuando en la resta hay un carry de bits, el resultado no se puede representar porque el sistema en el que se realizó la resta no lo permite.

Luego se resolvieron por grupos unas sumas y restas en la pizarra.

Se explicó el sistema hexadecimal, cuyos símbolos son los números del 0 al 9 y las letras de la A a la F.
Para interpretar en hexadecimal es como en binario, pero realizando multiplicaciones suscesivas en base 16.
I(12A) = 1 x 16^2 + 2 x 16^1 + A x 16^0 = 256 + 32 + 10 = 298

Y para representar una cadena también es como en binario pero se divide sucesivamente por 16 y luego se agrupan los restos del último al primero.

Se explicó lo que es la agrupación de bits, que es un método para pasar de binario a hexadecimal, que consiste en agrupar bits en conjuntos de a cuatro para interpretarlos y obtener un valor del sistema hexadecimal; este proceso a la inversa (interpretar un carácter en hexa) se utiliza para pasar de hexadecimal a binario.

Se realizaron los ejercicios 5 y 8 de la práctica 0

Cada grupo realizó un mapa conceptual de la clase y con eso concluyó la misma.

Se realizo la presentación de los alumnos brindandole un post it a cada uno para poder reconocer sus nombres y lo mismo se realizó con los profesores y ayudantes.

Se resolvieron unas preguntas sobre el cuento de los panes en ocho grupos armados al azar por los mismos alumnos, luego de realizarse la puesta en común de las respuestas dadas se mostró el video de la evolución de las computadoras, que se encuentra disponible acá

Se realizó una puesta en común de este video realizando una línea de tiempo en el pizarrón para los datos mas importantes.
Se introduce el concepto de la arquitectura de Von Neumann con un gráfico de como esta compuesta.

Luego de tomar un descanso se realizaron preguntas a todos los grupos sobre los sistemas de numeración para realizar una introducción al sistema binario.
Se explicó como interpretar cadenas binarias (compuestas por unos y ceros).
Por ejemplo:

I(011) = 0 x 2^2 + 1 x 2^1 + 1 x 2^0 = 0 + 2 + 1 = 3

Se realizó la explicación de como representar números con el método de las divisiones sucesivas, que consiste en dividir un número hasta que de cero y acumular los restos de esas divisiones, que son los símbolos que forman la cadena.

Para finalizar la clase, cada grupo pasó al pizarrón para resolver interpretaciones y representaciones.