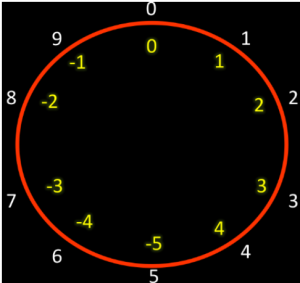
Comenzamos trabajando con un hipotético sistema de cadena decimal de un dígito.

Entonces, los dígitos con los respectivos valores que interpretan son:

Cadena: 0    1    2    3    4    5    6    7    8    9

Valor:     0    1    2    3    4   -5   -4   -3   -2   -1

Vemos que el rango es [-5, 4]

Lo interesante es que al sumar dos cadenas, la cadena resultante representa el valor correcto. Por ejemplo, 3 + 6 = 9. Si interpretamos esta expresión nos queda 3 + (-4) = (-1) lo cual es correcto.

Si a este sistema lo pasamos a cadena binaria de 3 dígitos nos quedará:

Cadena: 000 001 010 011 100 101 110 111

Valor:       0     1     2     3    -4    -3    -2    -1

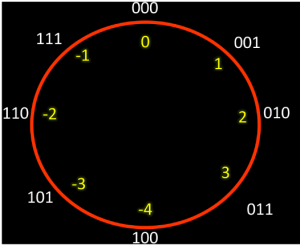Vemos que el rango es [-4,3]. Recordando que SM(3) tiene rango [-3,3], vemos que hemos ganado un valor representable (ya que tenemos una única cadena para el valor 0).

Dada una cadena, si queremos obtener su complemento (cadena de misma magnitud, diferente signo) deberemos de seguir estos pasos:

Entonces, dada la cadena 001 (que representa al 1), su complemento será:

• ¿Cómo interpretamos una cadena que empieza con 0 en CA2? Simplemente como veníamos interpretando en BSS.
  si C comienza con 0 entonces Ica2(C) = Ibss(C)
  
•  ¿Cómo interpretamos una cadena que empieza con 1 en CA2? Una manera es interpretando su complemento y luego multiplicarlo por (-1) (cambiarle el signo).
  si C comienza con 1 entonces Ica2(C) = -(1) x Ibss(comp(C))

• ¿Cómo representamos un número positivo en CA2? Simplemente como se representa en BSS. Ojo con el rango!
  si x>=0 entonces Rca2(x)= Rbss(x)
•  ¿Cómo representamos un número negativo en CA2? Para utilizar el mecanismo de representación conocido (BSS), debemos tomar su opuesto (o valor absoluto) y luego complementar la cadena resultante.
  si x<0 entonces Rca2(x)=comp( Rbss( |x| ) )

 Para el viernes: